La Habana, (PL) La solución del problema booleano de las ternas pitagóricas, enunciado hace 35 años, ocupa 200 terabytes, y fue resuelto por la supercomputadora Stampede de la Universidad de Texas en Estados Unidos (EE.UU.).
Por: Esther García*
Según los científicos, esta respuesta matemática tiene un tamaño equivalente a todos los textos digitalizados de la biblioteca del Congreso norteamericano; y un ser humano tardaría 10 mil millones de años en leerla.
El problema planteaba: ¿Es posible colorear cada entero positivo (1, 2, 3, 4, 5…) de azul o rojo de forma que en ninguna terna de enteros a, b y c que responde a la famosa ecuación de Pitágoras a2+b2=c2 sean todos del mismo color.
Con la colaboración de matemáticos ingleses, el equipo texano comprobó que es posible pintar cada número entero de rojo o azul evitando coincidencias de colores en cualquiera de las ternas.
Es decir, con la terna 3, 4 y 5, los números 3 y 5 deberían ser azules y el 4, rojo. Se ha demostrado que hay 102 mil 300 modos de colorear los números enteros hasta siete mil 824, pero una vez alcanzada esta cifra, es imposible tener ternas multicolores, explicó uno de los coautores de la investigación, Laurent Simon.
Simon dijo que para responder la interrogante de las ternas pitagóricas, se necesitaron los 800 procesadores de Stampede y un programa de su autoría denominado Glucose.
Pues básicamente, se ha demostrado que los números del 0 al 7824 se pueden colorear de 10²³ºº formas en las que se cumpla la norma, pero que a partir de ese número ya no se podrían conseguir ternas de dos colores.
Este problema fue enunciado por una supercomputadora en el año 1981 y desde entonces se trataba de darle una respuesta, que ha llegado recientemente de la mano de Marijn Heule, Oliver Kullman y Victor Marek, pertenecientes a las Universidades de Texas, Swansea y Kentucky.
¿Qué son las ternas pitagóricas?
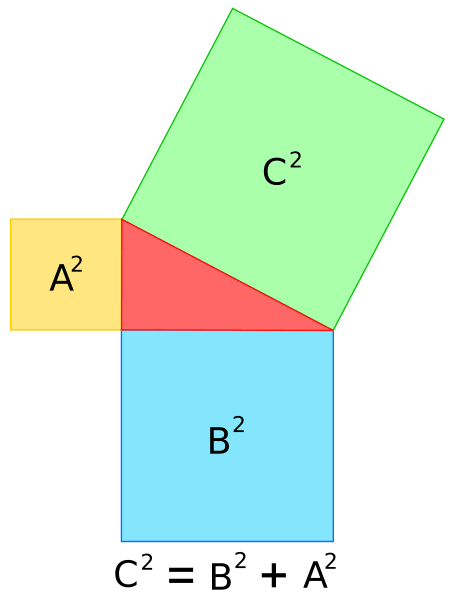
Una terna pitagórica consiste en una tupla de tres enteros positivos a, b, c que cumplen: a2+b2=c2.
El nombre deriva del teorema de Pitágoras, el cual plantea que en cualquier triángulo rectángulo, se cumple que x2+y2=z2 (siendo (x) y (y) las longitudes enteras de sus catetos y (z) la de la hipotenusa). En sentido contrario también se cumple, o sea, cualquier terna pitagórica se puede asociar con las longitudes de dos catetos y una hipotenusa, formando un triángulo rectángulo.
Por otro lado, las ternas pitagóricas se clasifican de dos maneras: primitivas y no primitivas. Una terna pitagórica primitiva es aquella en la que el máximo común divisor de a, b y c es 1. Si (a, b, c) es una terna pitagórica primitiva, se pueden construir infinitas ternas no primitivas (da, db, dc), donde d es un entero positivo.
Los triángulos que se construyen con una terna pitagórica no primitiva son siempre proporcionales a otro triángulo cuyos lados forman una terna pitagórica primitiva.
Existen más de una terna primitiva con el mismo número entero menor. El primer ejemplo de esto es el 20, el cual es el menor entero de dos ternas primitivas: (20, 21, 29) y (20, 99, 101). Además, cualquier número entero n > 2 puede ser miembro de una terna pitagórica, para n = 19 : ( 19 , 180 , 181 )
Sistemas Stampede al servicio de la ciencia
El sistema Stampede es uno de los más potentes del mundo, y hasta el momento ha corrido más de siete millones de simulaciones y trabajos de análisis de datos para decenas de miles de usuarios en el planeta, explica el director ejecutivo de TACC e investigador principal de los proyectos Stampede y Stampede 2, Dan Stanzione.
Algunas de las funciones desempeñadas por Stampede han sido: la determinación de los riesgos de terremotos para ayudar a establecer códigos en las viviendas y edificios comerciales.
Según Stanzione, este sistema será superado por el Stampede 2 bajo las directrices del Texas Advanced Computing Center estadounidense, en la Universidad este estado.
"La nueva versión duplicará su rendimiento y mejorará también la memoria, capacidad de almacenamiento y ancho de banda".
En el participaran las compañías Intel, Dell y Seagate, aportando procesadores como los Intel Xeon Phi, conocidos por el nombre de "Knights Landing", y la futura generación de Intel Xeon.
Además, se recurrirá a la arquitectura Intel Omni-Path y a la tecnología de memoria no volátil 3D XPoint.
Para la transformación de Stampede, la National Science Foundation aportó una financiación de 30 millones de dólares.
* La autora es periodista de la redacción de Ciencia y técnica de Prensa Latina.